Illustrative Mathematics - High School
Grade Levels: High School
PROGRAM FEATURES
PROGRAM FEATURES
IM Algebra 1, Geometry, and Algebra 2 lessons are designed with a focus on independent, group, and whole-class instruction, building mathematical understanding and fluency with all students. Teachers will also use Warm-ups and Cool-downs to help guide lesson pacing and planning.
Students who struggle in Algebra 1 are more likely to struggle in subsequent math courses and experience more adverse outcomes. The Algebra 1 Supports Course is designed to help students who need additional support in their Algebra 1 course. Each Algebra 1 Supports Course lesson is associated with a lesson in the Algebra 1 course. The intention is that students experience each Algebra 1 Supports lesson before its associated Algebra 1 lesson. The Algebra 1 Supports lesson helps students learn or remember a skill or concept that is needed to access and find success with the associated Algebra 1 lesson.
Why take advantage of print versions and Professional Learning options?
Kendall Hunt offers print versions of student workbooks, teacher guides, and teacher resources to make the most of the Illustrative Mathematics® curriculum. Our high-quality workbooks and guides allow teachers to easily follow along and instruct their students while also acting as an additional resource for “creating a world where learners know, use and enjoy mathematics.”
Shifting to a problem-based mathematics curriculum can be a difficult transition for many educators. Professional Learning combined with the digital and print IM math curriculum presents an avenue for teachers to grow and watch their students, in turn, mature into better mathematicians. The certified training also provides support and clarity to educators and administrators while creating an avenue of engagement and deeper understanding.
This isn’t your typical professional learning opportunity. IM Certified Training is taught by IM Certified Facilitators who understand that each teacher’s needs is unique. Districts select the professional learning experience that best meets their needs-from an introductory session, to year-long support, to a three-year development package that builds teacher, coach, and leader capacity.
Have questions and want to inquire about print and Professional Learning options? Please contact your sales consultant here.
Join our IM KHommunity
Connect with and share ideas within an exclusive network of fellow KH/IM teachers, coaches, and administrators via Facebook
Algebra I - Teacher Guides include Support Guide
Each lesson and Unit Tells a Story
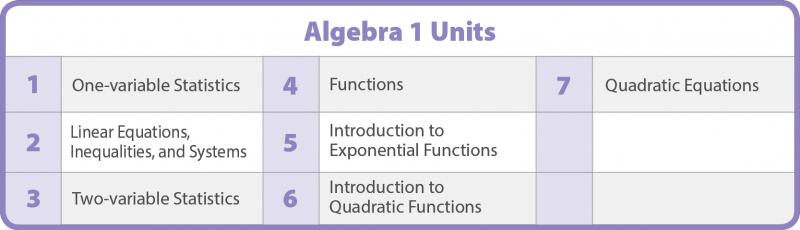
The story of Algebra 1 mathematics is told in seven units. Each unit has a narrative that describes the mathematical work that will unfold in that unit. Each lesson in the unit has a narrative. Lesson narratives explain:
- A description of the mathematical content of the lesson and its place in the learning sequence.
- The meaning of any new terms introduced in the lesson.
- How the mathematical practices come into play, as appropriate.
Activities within lessons also have a narrative, which explain:
- The mathematical purpose of the activity and its place in the learning sequence.
- What students are doing during the activity.
- What teacher needs to look for while students are working on an activity to orchestrate an effective synthesis.
- Connections to the mathematical practices when appropriate.
Launch - Work - Synthesize
Each classroom activity has three phases.
The Launch
During the launch, the teacher makes sure that students understand the context (if there is one) and what the problem is asking them to do. This is not the same as making sure the students know how to do the problem—part of the work that students should be doing for themselves is figuring out how to solve the problem.
Student Work Time
The launch for an activity frequently includes suggestions for grouping students. This gives students the opportunity to work individually, with a partner, or in small groups.
Activity Synthesis
During the activity synthesis, the teacher orchestrates some time for students to synthesize what they have learned. This time is used to ensure that all students have an opportunity to understand the mathematical goal of the activity and situate the new learning within students' previous understanding.
Practice Problems
Each lesson includes an associated set of practice problems. Teachers may decide to assign practice problems for homework or for extra practice in class. They may decide to collect and score it or to provide students with answers ahead of time for self-assessment. It is up to teachers to decide which problems to assign (including assigning none at all).
The practice problem set associated with each lesson includes a few questions about the contents of that lesson, plus additional problems that review material from earlier in the unit and previous units. Distributed practice (revisiting the same content over time) is more effective than massed practice (a large amount of practice on one topic, but all at once).
Are You Ready For More?
Select classroom activities include an opportunity for differentiation for students ready for more of a challenge. We think of them as the "mathematical dessert" to follow the "mathematical entrée" of a classroom activity.
Every extension problem is made available to all students with the heading "Are You Ready for More?" These problems go deeper into grade-level mathematics and often make connections between the topic at hand and other concepts. Some of these problems extend the work of the associated activity, but some of them involve work from prior grades, prior units in the course, or reflect work that is related to the K–12 curriculum but a type of problem not required by the standards. They are not routine or procedural, and they are not just "the same thing again but with harder numbers."
They are intended to be used on an opt-in basis by students if they finish the main class activity early or want to do more mathematics on their own. It is not expected that an entire class engages in Are You Ready for More? problems, and it is not expected that any student works on all of them. Are You Ready for More? problems may also be good fodder for a Problem of the Week or similar structure.
Instructional Routines
The kind of instruction appropriate in any particular lesson depends on the learning goals of that lesson. Some lessons may be devoted to developing a concept, others to mastering a procedural skill, yet others to applying mathematics to a real-world problem. These aspects of mathematical proficiency are interwoven. These materials include a small set of activity structures and reference a small, high-leverage set of teacher moves that become more and more familiar to teachers and students as the year progresses.
The first instance of each routine in a course includes more detailed guidance for how to successfully conduct the routine. Subsequent instances include more abbreviated guidance, so as not to unnecessarily inflate the word count of the teacher guide.
Digital Routines indicate required or suggested applications of technology, appearing repeatedly throughout the curriculum. Activities using the routines are flagged for the teacher, which is helpful for lesson planning and for focusing the work of professional development.
Some of the instructional routines, known as Mathematical Language Routines (MLR), were developed by the Stanford University UL/SCALE team. The purpose of each MLR is described here, but you can read more about supports for students with emerging English language proficiency in the Supporting English Language Learners section.
Analyze it
Anticipate, monitor, select, sequence, connect
Aspects of mathematical modeling
Card Sort
Construct It
Draw It
Extend it
Fit it
Math Talk
MLR4: Information gap cards
Notice and Wonder
Take turns
Think pair share
Which One Doesn’t Belong?
FOR EACH CLASSROOM/TEACHER
CUSTOMIZED SHOPPING FOR:
Algebra 1
ADD THE FOLLOWING:
Geometry - Teacher Guide includes Support Guide
Each lesson and Unit Tells a Story
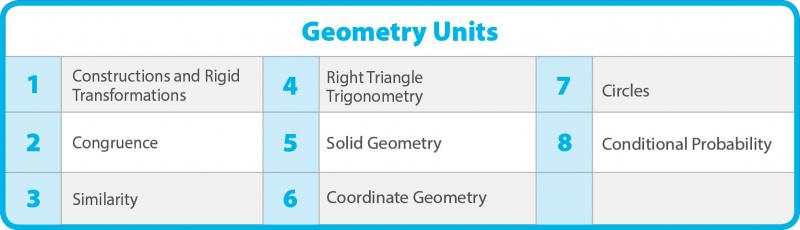
The story of Geometry is told in eight units. Each unit has a narrative that describes the mathematical work that will unfold in that unit. Each lesson in the unit has a narrative. Lesson narratives explain:
- A description of the mathematical content of the lesson and its place in the learning sequence.
- The meaning of any new terms introduced in the lesson.
- How the mathematical practices come into play, as appropriate.
Activities within lessons also have a narrative, which explain:
- The mathematical purpose of the activity and its place in the learning sequence.
- What students are doing during the activity.
- What teacher needs to look for while students are working on an activity to orchestrate an effective synthesis.
- Connections to the mathematical practices when appropriate.
Launch - Work - Synthesize
Each classroom activity has three phases.
The Launch
During the launch, the teacher makes sure that students understand the context (if there is one) and what the problem is asking them to do. This is not the same as making sure the students know how to do the problem—part of the work that students should be doing for themselves is figuring out how to solve the problem.
Student Work Time
The launch for an activity frequently includes suggestions for grouping students. This gives students the opportunity to work individually, with a partner, or in small groups.
Activity Synthesis
During the activity synthesis, the teacher orchestrates some time for students to synthesize what they have learned. This time is used to ensure that all students have an opportunity to understand the mathematical goal of the activity and situate the new learning within students' previous understanding.
Practice Problems
Each lesson includes an associated set of practice problems. Teachers may decide to assign practice problems for homework or for extra practice in class. They may decide to collect and score it or to provide students with answers ahead of time for self-assessment. It is up to teachers to decide which problems to assign (including assigning none at all).
The practice problem set associated with each lesson includes a few questions about the contents of that lesson, plus additional problems that review material from earlier in the unit and previous units. Distributed practice (revisiting the same content over time) is more effective than massed practice (a large amount of practice on one topic, but all at once).
Are You Ready For More?
Select classroom activities include an opportunity for differentiation for students ready for more of a challenge. We think of them as the "mathematical dessert" to follow the "mathematical entrée" of a classroom activity.
Every extension problem is made available to all students with the heading "Are You Ready for More?" These problems go deeper into grade-level mathematics and often make connections between the topic at hand and other concepts. Some of these problems extend the work of the associated activity, but some of them involve work from prior grades, prior units in the course, or reflect work that is related to the K–12 curriculum but a type of problem not required by the standards. They are not routine or procedural, and they are not just "the same thing again but with harder numbers."
They are intended to be used on an opt-in basis by students if they finish the main class activity early or want to do more mathematics on their own. It is not expected that an entire class engages in Are You Ready for More? problems, and it is not expected that any student works on all of them. Are You Ready for More? problems may also be good fodder for a Problem of the Week or similar structure.
Instructional Routines
The kind of instruction appropriate in any particular lesson depends on the learning goals of that lesson. Some lessons may be devoted to developing a concept, others to mastering a procedural skill, yet others to applying mathematics to a real-world problem. These aspects of mathematical proficiency are interwoven. These materials include a small set of activity structures and reference a small, high-leverage set of teacher moves that become more and more familiar to teachers and students as the year progresses.
The first instance of each routine in a course includes more detailed guidance for how to successfully conduct the routine. Subsequent instances include more abbreviated guidance, so as not to unnecessarily inflate the word count of the teacher guide.
Digital Routines indicate required or suggested applications of technology, appearing repeatedly throughout the curriculum. Activities using the routines are flagged for the teacher, which is helpful for lesson planning and for focusing the work of professional development.
Some of the instructional routines, known as Mathematical Language Routines (MLR), were developed by the Stanford University UL/SCALE team. The purpose of each MLR is described here, but you can read more about supports for students with emerging English language proficiency in the Supporting English Language Learners section.
Analyze it
Anticipate, monitor, select, sequence, connect
Aspects of mathematical modeling
Card Sort
Construct It
Draw It
Extend it
Fit it
Math Talk
MLR4: Information gap cards
Notice and Wonder
Take turns
Think pair share
Which One Doesn’t Belong?
FOR EACH CLASSROOM/TEACHER
FOR EACH STUDENT
CUSTOMIZED SHOPPING FOR:
Geometry
ADD THE FOLLOWING:
Algebra II - Teacher Guide (includes Support Guide)
Each lesson and Unit Tells a Story
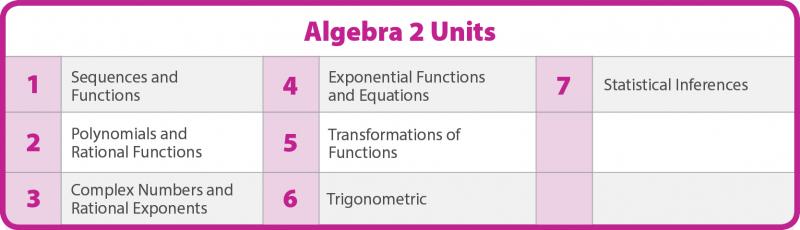
The story of Algebra 2 mathematics is told in seven units. Each unit has a narrative that describes the mathematical work that will unfold in that unit. Each lesson in the unit has a narrative. Lesson narratives explain:
- A description of the mathematical content of the lesson and its place in the learning sequence.
- The meaning of any new terms introduced in the lesson.
- How the mathematical practices come into play, as appropriate.
Activities within lessons also have a narrative, which explain:
- The mathematical purpose of the activity and its place in the learning sequence.
- What students are doing during the activity.
- What teacher needs to look for while students are working on an activity to orchestrate an effective synthesis.
- Connections to the mathematical practices when appropriate.
Launch - Work - Synthesize
Each classroom activity has three phases.
The Launch
During the launch, the teacher makes sure that students understand the context (if there is one) and what the problem is asking them to do. This is not the same as making sure the students know how to do the problem—part of the work that students should be doing for themselves is figuring out how to solve the problem.
Student Work Time
The launch for an activity frequently includes suggestions for grouping students. This gives students the opportunity to work individually, with a partner, or in small groups.
Activity Synthesis
During the activity synthesis, the teacher orchestrates some time for students to synthesize what they have learned. This time is used to ensure that all students have an opportunity to understand the mathematical goal of the activity and situate the new learning within students' previous understanding.
Practice Problems
Each lesson includes an associated set of practice problems. Teachers may decide to assign practice problems for homework or for extra practice in class. They may decide to collect and score it or to provide students with answers ahead of time for self-assessment. It is up to teachers to decide which problems to assign (including assigning none at all).
The practice problem set associated with each lesson includes a few questions about the contents of that lesson, plus additional problems that review material from earlier in the unit and previous units. Distributed practice (revisiting the same content over time) is more effective than massed practice (a large amount of practice on one topic, but all at once).
Are You Ready For More?
Select classroom activities include an opportunity for differentiation for students ready for more of a challenge. We think of them as the "mathematical dessert" to follow the "mathematical entrée" of a classroom activity.
Every extension problem is made available to all students with the heading "Are You Ready for More?" These problems go deeper into grade-level mathematics and often make connections between the topic at hand and other concepts. Some of these problems extend the work of the associated activity, but some of them involve work from prior grades, prior units in the course, or reflect work that is related to the K–12 curriculum but a type of problem not required by the standards. They are not routine or procedural, and they are not just "the same thing again but with harder numbers."
They are intended to be used on an opt-in basis by students if they finish the main class activity early or want to do more mathematics on their own. It is not expected that an entire class engages in Are You Ready for More? problems, and it is not expected that any student works on all of them. Are You Ready for More? problems may also be good fodder for a Problem of the Week or similar structure.
Instructional Routines
The kind of instruction appropriate in any particular lesson depends on the learning goals of that lesson. Some lessons may be devoted to developing a concept, others to mastering a procedural skill, yet others to applying mathematics to a real-world problem. These aspects of mathematical proficiency are interwoven. These materials include a small set of activity structures and reference a small, high-leverage set of teacher moves that become more and more familiar to teachers and students as the year progresses.
The first instance of each routine in a course includes more detailed guidance for how to successfully conduct the routine. Subsequent instances include more abbreviated guidance, so as not to unnecessarily inflate the word count of the teacher guide.
Digital Routines indicate required or suggested applications of technology, appearing repeatedly throughout the curriculum. Activities using the routines are flagged for the teacher, which is helpful for lesson planning and for focusing the work of professional development.
Some of the instructional routines, known as Mathematical Language Routines (MLR), were developed by the Stanford University UL/SCALE team. The purpose of each MLR is described here, but you can read more about supports for students with emerging English language proficiency in the Supporting English Language Learners section.
Analyze it
Anticipate, monitor, select, sequence, connect
Aspects of mathematical modeling
Card Sort
Construct It
Draw It
Extend it
Fit it
Math Talk
MLR4: Information gap cards
Notice and Wonder
Take turns
Think pair share
Which One Doesn’t Belong?
FOR EACH CLASSROOM/TEACHER
FOR EACH STUDENT
CUSTOMIZED SHOPPING FOR:
Algebra II
ADD THE FOLLOWING:
FOR EACH CLASSROOM/TEACHER
CUSTOMIZED SHOPPING FOR:
Algebra 1 Supports
ADD THE FOLLOWING:
Performed by IM Certified® Facilitators, we’ll make sure that the transition into a problem-based curriculum is comprehensive and easy for educators to implement.
IM® Professional Learning Features:
-
Designed to Support Shifts in Instructional Practice: Moving to a problem-based mathematics curriculum represents a significant practice shift for many educators. IM Professional Learning certified by IM guides teachers through the meaningful paradigm shifts that lead to improved student outcomes.
-
Delivered by Master Educators: IM Certified Facilitators undergo a rigorous qualification and training process to gain mastery in delivering impactful learning experiences based on the author’s intent.
-
Sustainable, Scalable Learning: IM Certified learning is tailored to meet teachers where they are on the learning continuum, allowing educators at every level to develop their skills over time. Districts select the learning experience that best meets their needs—from an introductory session, to year-long support, to a three-year development package that builds teacher, coach, and leader capacity.
-
Proven to Boost Educator Effectiveness: Our suite of professional tools helps teachers develop the skills and confidence to implement standards-aligned instruction, ensure curricular coherence within and across grade levels, facilitate meaningful mathematics discussions, and implement instructional routines that engage students and improve their learning.
Take a looking at the catalog of IM Professional Learning offerings.
CUSTOMIZED SHOPPING FOR:
IM 9-12 Professional Learning
ADD THE FOLLOWING:
Assess Learning, Analyze Data, and Differentiate Math Instruction with ASSISTments
ASSISTments, a free digital learning platform, makes it possible to transform ordinary assignments into powerful learning experiences, helping teachers be more responsive to students in real-time and helping students succeed. This virtual solution seamlessly pairs with the Illustrative Mathematics® curriculum to make learning accessible from anywhere. Together, Kendall Hunt and ASSISTments are ready to help your students achieve more.
Using the IM Math curriculum in ASSISTments, teachers can…
- Assign the Practice Problems for each lesson as in-class or at-home independent practice.
- Foster math conversations around Student Tasks and common wrong answers found in the assignment report.
- Finish each lesson by assigning a Cool Down and use the immediate data to help inform your instruction.
- Assign your Unit Assessments to get quick, real-time data on whole class successes and challenges.
- Plus, so much more!
Tell Me More about how I can incorporate ASSISTments into my classroom.
